tech-interview
Data Structures
Data Structures is one of the key area which developers must focus while preparing technical interviews. I have put together minimum and the most common data structures
- Arrays
- List
- Array vs Array List vs Linked List
- Map
- Set
- List vs Map vs Set
- Stack
- Queue
- Tree
- Heap
- Graph
Array
Array is the most important data structure and is the base for many other data structures. Thus, it is important to understand it and how they behave in memory.
I always believed that I understand arrays well enough and they are not crucial to practice anymore. Well, I was wrong since many years after I started working.
I observed that it was difficult for me to solve array problems because I tend to underestimate them. I was not even able to solve slightly complex array problems.
The reason being, my knowledge about arrays was incomplete.
You don't make the same mistake. Learn and practice arrays. Try solving array problems even if you think you do understand them properly.
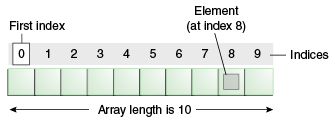
What is an array?
A group of elements of same type stored at contagious memory locations. That’s it. Let’s understand what this means. Before we use array, they need to be
- declared
- allocated with memory of predefined size (no of elements to store)
- size can’t be altered
Array Declaration
This is how we declare an array. arr is a local variable created on stack memory to hold integers. It does not point to anything yet.
int[] arr;
Array Initialization
This is when memory is reversed for elements on the heap and memory location of 1st element is stored as a
reference in arr variable on stack. It is called base address of an array.
arr = new int[5];
generally, we do declaration and memory allocation in a single step as follows
int[] arr = new int[5];
At this moment array is created with 5 elements but what those element look like? What value do they contain? Did
you try printing them? Well, since it is an integer array, elements are initialized with int default value of zero.
Memory Allocation
Let say for 5 integer elements, memory is reserved from 101 to 120 considering integer is of 4 bytes. The memory address of 101 is stored in local variable as a reference. When suppose 2nd index is requested, memory location is calculated using base address.
// for one dimensional array
base address + (index * size of integer)
101-104 for element 1 >> 101 + (0 * 4) = 101
105-108 for element 2 >> 101 + (1 * 4) = 105
109-112 for element 3 >> 101 + (2 * 4) = 109
113-116 for element 4 >> 101 + (3 * 4) = 113
117-120 for element 5 >> 101 + (4 * 4) = 117
// for two dimensional array
base address + (row * columns in row * size of integer) + (column * size of integer)
Insert
Inserting an element in array is a constant time operation O(1)
arr[0] = 5;
arr[1] = 10;
arr[2] = 15;
arr[3] = 20;
arr[4] = 25;
Note the arrays special syntax. Array needs to know the index for performing it’s operations. Based on index, it calculates the location into reserved memory and does it’s job.
Retrieve
Similar to adding, retrieving element from an array is also a constant time operation O(1)
int element3 = arr[2];
int element5 = arr[4];
Delete
Deleting an element from an array is NOT a constant time operation. It requires us to move other elements to the left by 1. Hence, it is amortized linear time operation O(N)
For example, to delete 3rd index element from 5 elements array, we have to move 4th & 5th element into 3rd and 4th position. There is no way to pass an index and ask array to delete it.
arr[3] = ? // what shall we say here to delete it
Extra Point: Deleting an element from an array does not shrink the array size.
Search
Searching an element in array is a linear time operation O(N). We have to iterate through array elements to look for value. In worst case, we may have searched an entire array and found nothing.
Extra Point: Searching an element in the ordered array is O(Log N) operation using binary search technique.
Array Example
References
[1]
[2]
List
- Use list when sequence matters
- List is an interface. ArrayList & LinkedList are implementations
References [1] [2] [List Implementations]
Array List
- Array List happens to be strong where Array is weak.
- ArrayList internally keeps an array to hold elements
- Arrays are fixed in size whereas ArrayList size grows dynamically with reallocation process
- ArrayList is an object, it has state and behavior whereas array is not an object but has special syntax
You must initialize ArrayList with capacity especially for large inputs, this also reduce reallocation iterations.
Insert
- Adding an element is O(1) as it always adds element at last.
- Adding N elements takes O(N) time.
- List interface provide ways to add element at a specified index which is O(N)
Retrieve
- Retrieving an element is O(1) since it is backed by array and requires an index
Delete
- Deleting element is O(N), requires an index and has to move elements to the left of deleted index
Search
- Searching an element is a linear time operation O(N)
Linked List
- Linked List happens to be strong where Array & Array List is weak.
- Gives flexibility to add/delete elements in middle of the list in a constant time
- Searching is still O(N)
Linked List elements are not stored in contagious memory locations as the case with arrays. Instead, Linked List has a property where each element contains the location of next and/or previous element.
- maintains head and tail pointers to iterate
- maintains the length of list - number of elements
- based on index, it may start from head or tail and gives O(Log N) time performance
Insert
- Insert item is O(1) as it insert item at tail
- Insert item at index is O(Log N) as in
- iterate to the index - O(Log N)
- create new node - O(1)
- manipulate pointers - O(1)
Retrieve
- Retrieving element is O(N) as it requires to search the element first.
- Retrieving element by index is O(N) as it takes linear time O(N) to reach the index. This can be reduced to O(Log N)
Delete
- Deleting element is O(N) as it requires to search the element first.
- Deleting element by index is O(N) as it takes linear time O(N) to reach the index. This can be reduced to O(Log N)
Search
- Searching an element is a linear time operation O(N) and can be reduced to O(Log N)
Linked List Example
Basic Implementation
Basic Implementation Tests
Array vs Array List vs Linked List
| Array | Array List | Linked List | |
|---|---|---|---|
| properties | * items are stored in contagious memory locations on heap * memory of given size reserved at declaration time * has fixed size * has special syntax * good for adding item, retrieving item by index, searching item in ordered array * bad at inserting in middle, deleting item or searching unordered items |
* resizable data structure backed by array * since flexible but consider reallocation function * initialized with default capacity * ensure capacity for large input as reallocation affects performance * good as an array, advantage is the dynamic size |
* list where each item keeps a reference to next/prev item * flexible in size * good at adding or removing item in middle of list * bad at searching item |
| Insert item | O(1) - takes an index & value | O(1) - adds at end | O(1) - adds at end |
| Insert item at | O(1) - update value at given index | O(N) - shift items to right | O(Log N) - iterate to given index from head or tail, add item, update pointers |
| Retrieve item | O(N) - iterate through array to find | O(N) - iterate through array | O(N) - iterate through list |
| Retrieve item at | O(1) | O(1) | O(Log N) - iterate to given index from head or tail |
| Delete item | ~ | O(N) - first search item index | O(N) - search for item and update pointers |
| Delete item at | O(1) - this does not change size | O(N) - shift items | O(Log N) - iterate to given index and update pointers |
| Search item | * Linear time O(N) * O(Log N) for ordered items using binary search technique |
Linear time O(N) | Linear time O(N) |
Map
- Use map when finding item with key matters
- Map is an interface and HashMap & HashTable are implementation
- Map keys to values
- Map cannot contain duplicate keys
How does Map work? Map takes a key,value pair
References [1] [2] [Map Implementations]
HashMap
Insert
*
Retrieve
*
Delete
*
Search
*
Set
- Use set when uniqueness matters
- Set is an interface and HashSet is an implementation
References [1] [2] [Set Implementations]
HashSet
Insert
*
Retrieve
*
Delete
*
Search
*
List vs Map vs Set
| List | Map | Set | |
|---|---|---|---|
| Insert | O(1) | O(1) | O(1) |
| Retrieve | O(1) | O(1) | O(1) |
| Delete | O(N) | O(1) | O(1) |
| Search | O(N) | O(1) | O(1) |
Must Read [1]
Stack
- LIFO > Last-In-First-Out
-
FILO > First-In-Last-Out
##### Applications #####
- reverse a word
- undo operation in text editors
- back button on browser
- function call
- depth first search
| Insert | Retrieve | Delete | Search |
|---|---|---|---|
| O(1) | O(1) | O(1) | O(N) |
Basic Stack
Basic Stack Tests
Generic Stack
Generic Stack Tests
References [1] [2] [Stack Implementations]
Queue
- FIFO > First-In-First-Out
-
LILO > Last-In-Last-Out
##### Applications #####
- message processing
- Breadth First Search
- batch jobs
- priority queues (discussed later)
| Insert | Retrieve | Delete | Search |
|---|---|---|---|
| O(1) | O(1) | O(1) | O(N) |
References [1] [2] [Queue Implementations]
Tree
Tree Traversal
Tree Traversal Tests